编译原理 - 华保健

编译器结构

未优化的编译器结构

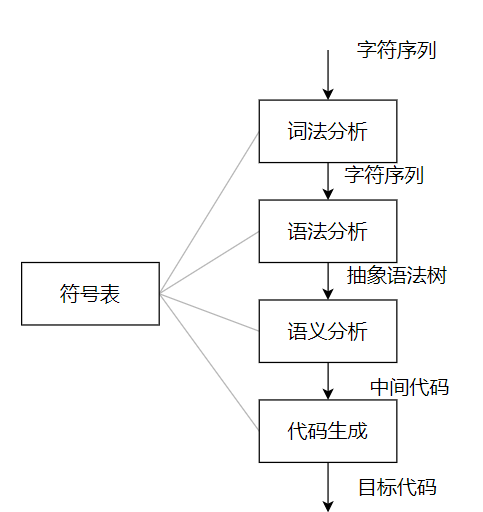
小结：

1. 编译器由多个阶段组成，每个阶段都要处理不同的问题
   1. 使用不同的理论、数据结构和算法
2. 编译器设计中的重要问题是如何合理的划分组织各个阶段
   1. 接口清晰
   2. 编译器容易实现、维护

任务： 编译程序 1+2+3 到栈式计算机

词法分析

词法分析的任务

这样一个流程，先通过词法分析，然后语法分析，再就是语义分析

通过词法分析器，将代码的文本转化为特定的记号。例如，if 转成 IF枚举，放到树中。变量变成 结构ID(变量)，放到数中。

这是记号的数据结构

enum kind{ IF, LPAREN, ID, INTLIT, ...};

struct token {
    enum kind k;  // 记号
    char *lexeme; // 记号对应的单词
}

例子：

if(x < 5)

转为为

token { k = IF, lexeme = 0 }  // 0 为空
token {k = LPAREN, lexeme = 0 } // 左括号
token {k  = ID, lexeme = "x" } // 变量值
token {k = LESS, lexeme = "<" } // 小于
token {k = INT, lexeme = "5" }
token {k = RPAREN, lexeme = ")"}

小结

词法分析器的任务：字符流到记号流

• 字符流：
  • 和被编译的语言密切相关（ASCII, Unicode, or … )
• 记号流：
  • 编译器内部定义的数据结构，编码所识别出的词法单元

词法分析的实现方法

• 至少两种实现方案
  • 手工编码实现法
    • 相对复杂、且容易出错
    • 目前非常流行的实现方法： GCC、LLVM
  • 词法分析器生成器
    • 可快速原型，代码量较少
    • 但较难控制细节

转移图

这个图就是识别符号，将符号转成记号的核心逻辑。

生成的伪代码：

token nextToken()
    c = getchar();
    switch(c):
        case '<':
            c = getchar();
            switch(c):
               case '=': return LE;
               case '>': return NE;
               default: rollback(); return LT;
        case '=': return EQ;
        case '>':
            c = getchar();
            switch(c):
               case '=': return GE;
               default: rollback(); return GT;

标识符转移图

标识符和关键字

• 很多语言中标识符和关键字有交集
  • 从词法分析的角度看，关键字是标识符的 一部分
• C以语言为例
  • 标识符：以字母或下划线开头，后跟多个字母、下划线、或数字
  • 关键字: if while else switch case …

识别关键字

例子: ifxy

关键字表算法

就是先按转移图把所有标识符搞出来，然后在表中查到哪些是关键字，再作处理。

• 对给定语言中所有的关键字，构造关键字构成的哈希表H
• 对所有识别的标识符和关键字，先统一按标识符的转移图进行识别
• 识别完后，再到表H 中找到关键字
• 通过合理的构造哈希表H（完美哈希），可以O(1) 时间完成。

自动生成器

正则表达式

• 对给定的字符集 ∑ = {c1, c2, … cn }
• 归纳定义：
  • 空串 e 是正常表达式
  • 对于任意 C ∈ ∑ ， C 是正则表达式
  • 如果M 和N 是 正则表达式，则以下也是正则表达式
    • 选择 M | N = { M, N }
    • 连接 MN = {mn | m ∈ M，n ∈ N}
    • 闭包 M* = {e, M, MM, MMM, …. } ∞

1. 例子：关键字

C语言中的关键字 如 if , while 如何使用正则表达式表示？

∑ = ASCII

if , i ∈ ∑ ， f ∈ ∑

1. 例子：标识符

C语言中的标识符以 字母、数字、下划线开头，后面跟零个或多个字母、数字、下划线。

正则表达式如下：

① (a|b|c|d|e….|z|_)

② (a|b|c|d|e…|z|A|B|C|D|E….|Z|_)

1. 例子：C 语言中的无符整数

正则如下:

(0|1|2|3|4|5|6|7|8|9)

语法粮

引入语法糖来简化构造

• [ c1 - cn] == c1 | c2 | …. | cn
• e+ == 一个或多个 e
• e? = 零个或多个e
• “a*” == a* 自身，不是 a的kleen闭包*
• e {i,j} == i 到 j 个e的连接
• . == 除 \n 外的任务字符

状态自动机

有限状态自动机（FA）

M = (∑, S, q0, F, δ）

∑ 字母表

S 状态集

q0 初始状态

F 终结状态集

δ 转移函数

自动机例子

写一个字串如

S = “aabb”

放到下面的自动机当中，看有能不能有结果，如果没有结果，那么说明该自动机不能接受这个字符串

转移函数:

M = { ∑ ， S， q0 ， F，δ ｝

∑ = { a, b }

S = ｛0， 1， 2｝

q0 = 0

F = ｛2｝

δ = { (q0, a) → q1, (q0, b) → q0, (q1, a) → q2, (q1, b) → q1, (q2, a) → q2 , (q2 , b) → q2 }

有限状态自动机小结

• 确定状态有限自动机 DFA
  • 对任意的字符，最多一个状态可以转移
    • δ： S x ∑ → S
• 非确定的有限状态自动机 NFA
  • 对任意字符有多余一个状态可以转移
    • δ： S x ( ∑ ∪ ε ) → ζ（S）

这是一个有向图，每一个节点 会 附带 信息，

状态\字符	a	b
0	1	0
1	2	1
2	2	2

RE 转换成 NFA —— Thompson算法

Thompson 算法

• 基于对RE的结构做归纳
  • 基于基本的RE直接构造
  • 对复合的RE递归构造
• 递归算法，容易实现
  • 我这里实现，不到100行代码

NFA 转 DFA - 子集构造算法[未完成]

这里主要讲的是 子集构造算法

两个算法没怎么听懂，云里雾里。后面再补这一节内容。

DFA 最小化 - Hopcroft 最小化算法

基于等价类的思考，把DFA 分成几块，根据其输入和最终状态。

比如下面的一个图，相当于直接可以简化成两个结点。

示例1

split(s)
    foreach( character c)
        if (c can split s) 
            split S into T1, ... , TK

hopcroft()
    split all nodes into N,A
    while( set is still changes)
        split(s)

示例2

我的感觉就是相当于把一些结点进行整合了，像相同输入条件的最终状态，直接变成一个结点。

DFA 代码表示

这一节主要的感觉就是将 DFA 变成一个二维表，也就是说DFA 和NFA 的图难道需要提前画好，然后手动用二维表进行操作吗。目前的感觉是这样的。

• 概念上，DFA是一个有向图
• 实际上，DFA有不同的代码表示
  • 转移表（类似于邻接矩阵）
  • 哈希表
  • 跳转表
• 取决于在实际实现中，对空间的权衡

转移表

转移表就是将DFA以二维表的形式进行表示，然后存放在 实际的二维表中。

状态/字符	a	b	c
0	1
1		1	1

char table[M][N];

table[0]['a'] = 1;
table[1]['b'] = 1;
table[1]['c'] = 1;
// other table entries are error

驱动代码

nexToken()
    state  = 0
    stack = []
    while (state != ERROR)
        c = getChar()
        if (state is ACCEPT)
            clear(stack)
        push(state)
        state = table[state][c]

    while(state is not ACCEPT)
        state = pop();
        rollback();

最长匹配

可以把这样一个有向图，的方向用算法进行匹配，我的感觉就是要匹配所有的字符串麻。

一个DFA 匹配一个。这显然可能只是一个分支。

而关键字是 ifif ，而不能直接使用简单的if，因为如果是ifii是无法通过此状态机的，如果使用的ifif才行。

nextToken()
    state = 0
    stack = []
    while (state != ERROR)
        c = getChar()
        if( state is ACCEPT)
            clear(stack)
        push(state)
        state = table[state][c]

    while(state is not ACCEPT)
        state = pop();
        rollback();

跳转表

状态/字符	a	b	c
0	1
1		1	1

nextToken()
    state = 0
    stack = []
    goto q0
    
    q0:
    c = getChar()
    if( state is ACCEPT)
        clear(stack)
    push(state)
    if(c == 'a')
        goto q1

    q1:
    c = getChar()
    if(state is ACCEPT)
        clear(stack)
    push(state)
    if( c == 'b' || c == 'c')  
        goto g1                  // 这里不用递归调用吗         

语法分析

语法树的构建

if(x > 5)
    y = "hello"
else
    z = 1;

路线图

• 数学理论：上下文无关文法（CFG）
  • 描述语言语法规则的数学工具
• 自顶向下分析
  • 递归下降分析算法（预测分析算法）
  • LL分析算法
• 自底向上分析
  • LR分析算法

上下无关文法和推导

历史背景：乔姆斯基文法体系

为研究自然语言构造的一系列数学工具

示例

• 自然语言中句子的典型结构
  • 主语 谓语 宾语
  • 名字 动词 名词
• 例子：
  • 名词：｛羊、老虎、草、水｝
  • 动词：｛吃、喝｝

形式化

非终结符：{S，N，V}

终结符：{s,t,g,w,e,d}

开始符：S

S -> N V N
N -> s
    | t
    | t
    | g
    | w
V -> e
    | d

介绍

上下文无关文法G 是一个四元组：

G = ( T, N, P, S)

其中T 是终结符集合

N 是非终结符集合

P 是一组产生式规则

每条规则的形式: X-> β1 β1 … βn

其中 X ∈ N , βi ∈ ( T U N）

S 是唯一开始的符号 （非终结符）

S ∈ N

上下无关文法的例子

G = （T， N ，P， S）

非终结符 N = {E}

终结符： T = {num, id, +, *}

开始符号：E

产生式规则集合:

E -> num
E -> id
E -> E + E
E -> E * E

一般把 `E->`省略成 `|`
E -> num
    | id
    | E + E
    | E * E

推导

• 给定文法G，从G的开始符号S开始，用产生式的右部替代左侧的非终结符
• 此过程一直重复，直到不出现非终结符为止
• 最终的串称为句子

例子：

S -> N V N 
N -> s
    | t
    | g
    | w
V -> e 
    | d

下面的是替换的步骤
1. S -> N V N
2. S -> N d N 
3. S -> N d s
4. S -> w d s

最左推导和最右推导

最左推导：每次问题选择最左侧的符号进行替换

S -> N V N 
N -> s
    | t
    | g
    | w
V -> e 
    | d

下面的是替换的步骤
1. S -> N V N
2. S -> s V N
3. S -> s d N 
4. S -> s d w

语法分析

给定方法 G 和 句子 s, 语法分析要回答的问题： 是否存在对句子 s 的推导

S -> N V N 
N -> s
    | t
    | g
    | w
V -> e 
    | d

下面两个例子是否存在 对句子s 的推导？
S = s d s [YES]
S = s s s [NO] 

分析树和二义性文法

分析树

• 推导可以表达成树状结构
  • 和推导使用的顺序无关（最左、最右、其他）
• 特点：
  • 树中的每个内部结点，代表非终结符
  • 每个叶子节点代表终结符
  • 每一步推导代表如何从双亲节点生成它的孩子节点

表达式的例子

这个遍历的顺序和 树的乘法的优先级 都会直接影响计算结果，这也就是 二义性文法

分析树的含义解决于树的后序遍历。

二义性文法

• 给定文法G，如果存在句子s，它有两棵不同的分析树，那么称G 是二义性文法
• 从编译器角度，二义性文法存在问题：
  • 同一个程序会有不同的含义
  • 因此程序运行的结果不是唯一的
• 解决方案：文法的重写

表达式文法的重写

E -> E + T
    | T
T -> T * F
    | F
F -> num
    | id

推导: 3 + 4 * 5

E -> E + T
    -> T + T
    -> F + T
    -> 3 + T 
    -> 3 + T * F
    -> 3 + F * F
    -> 3 + 4 * F
    -> 3 + 4 * 5

相当于一个转换，把 T 与 F 进行定义，然后在进行表达式的代入。

为什么 T 会变成 F 呢？ 因为 3 单独来看在 T 这个文法中，若为单独一个数字则是 F。

 其实是 T + T * T

推导 3 + 4 + 5

使用 左结合

E -> E + T 
    -> E + T + T
    -> T + T + T
    -> F + T + T
    -> 3 + T + T
    -> 3 + F + T
    -> 3 + 4 + T
    -> 3 + 4 + F
    -> 3 + 4 + 51

自顶向下分析

算法思想

• 语法分析：给定文法G和句子s，回答s是否能够从G推导出来？
• 基本算法思想：从G的开始符号出发，随意推导出某个句子t，比较t和s
  • 若 t == s 则回答 “是”
  • 若 t != s 则 ? （不能直接回答否）
• 因为这是从开始符号推断句子，因此称为自称向下分析
  • 对应于分析树自顶向下的构造顺序

如果推导不成功，是需要回溯的。

这个大写的S 的名词为规则，在树中也是一个结点。当推导不成功时，回溯到S结点，再选择其他的规则。

S -> N V N 
N -> s
    | t
    | g
    | w
V -> e
    | d

如果 N V N 这个规则推不出来，则要回溯到其他 规则结点

代码

这个是用栈来做显示的后序遍历

tokens[]; // holding all tokens
i = 0;
stack = [S] // S 是开始符号
while (stack != [])
    if (stack[top] is a terminal t)
        if ( t == token[i++])
            pop();
        else rollback();
    else if (stack[top] is a nonterminal T)
        pop(); push(the next right hand side of T)

看栈中的s，发现s 没有匹配成功，所以需要回溯。回溯就是需要重新回到N1

算法的讨论

• 算法需要用到回溯
  • 给分析效率带来问题
• 就这部分而言，编译器必须高效
  • 编译上千万行代码的内核等程序
• 因此，我们需要线性时间的算法
  • 避免回溯
  • 引出递归下降分析算法 和 LL(1)分析算法。

“用前看符号避免回溯”

递归下降分析算法

• 也称预测分析
  • 分析高效（线性时间）
  • 容易实现（方便手工编码）
  • 错误定位 和 诊断信息准确
  • 被很多开源和商业的编译器所采用
    • GCC 4.0 , LLVM 。。。
• 算法基本思想
  • 每个非终结符构造一个分析函数
  • 用前看符号指导产生规则的选择

算法

在实现的算法的时候，更像是一个分治法

推导: g d w 

S -> N V N 
N -> s
    | t
    | g
    | w
V -> e
    | d

// 伪代码
parse_S()
    parse_N()
    parse_V()
    parse_N()

parse_N()
    token = tokens[i++]
    if (token == s || token == t || token == g || token == w )
        return;
    error("...")

parse_V()
    token = tokens[i++]
    if( token == e || token == d)
        return ;
    error(".... parse_V")

一般算法框架

parse_X()
    token = nextToken()
    switch(token)
        case ...: // β11 ... β1i
        case ...: // β21 ... β2i
        case ...: // β31 ... β3i
        ...
        default: error("...");


///////////////////
文法如下
x -> β11 ... β1i
    | β21 ... β2i
    | β31 ... β3i
    

对算术表达式的递归下降分析

parse_E()
    token = nextToken()
    if (token == num)
        ? // E + T
    else error("...")

E -> E + T
    | T
T -> T * F
    | F
F -> num 

num就是终结符

parse_E()
    parse_T()
    token = tokens[i++]
    while(token == '+')
        parse_T()
        token = tokens[i++]
    
parse_T()
    parse_F()
    token = tokens[i++]
    while(token == '*')
        parse_F()
        token = tokens[i++]

LL(1)分析算法

• 从左（L）向右读入程序，最左（L）推导，采用一个（1）前看符号
  • 分析高效（线性时间）
  • 错误的定位和诊断信息准确
  • 有很多开源或商业的生成工具
    • ANTLR
• 算法的基本思想
  • 表驱动的分析算法

表驱动的LL分析器架构

0: S -> N V N
1: N -> s 
2:    | t
3:    | g
4:    | w
5: V -> e
6:     |d


分析: g d w

N\T	s	t	g	w	e	d
S	0	0	0	0
N	1	2	3	4
V					5	6

因为存放数据的时候使用提栈，而S 是文法的开始符。

所以如果 是 g g d

那么 g开头，则是 表[S,g] = 0，因为是开始符

然后再取 表[N,g] = 3 ，这个直接跳过了回溯。是直接在文法定义阶段可以确定的固定数据。

这个为0，就是因为 文法的 S -> N V N，N放在首位

算法伪代码

tokens[];
i = 0;
stack  = [S]
while(stack != [])
    if( stack[top] is a terminal t)
        if(t == tokens[i++])
            pop();
        else error(...)
    else if(stack[top] is a nonterminal T)
        pop(); push(the correct right hand side of T)
                                        table[N,T]

FIRST集

定义：

FIRST(N) = 从非终结符N开始推导得出句子开头所有可能终结符的集合

对 N -> a

FIRST(N) ∪ = {a}

对 N -> M

FIRST(N) ∪ = FIRST(M)

FIRST集的不动点算法

• 回答为什么这个算法会终止
  • 当所有的非终于符都做好了放到FISRT集了后
  • FIRST集理应不会发生变化
  • 所以while条件退出

foreach(nonterminal N)
    FIRST(N) = {}

while (some set is changing)
    foreach( production p: N-> β1 ... βn)
        if( β1 == a ... )
            FIRST(N) U= {a}
        if (β1 == M ...)
            FIRST(N) ∪ FIRST(M)

0: S -> N V N
1: N -> s 
2:    | t
3:    | g
4:    | w
5: V -> e
6:     |d

把上面的文法，使用FISRT集的不动点算法可得出一个新的数据结构

N\FIRST	0	1	2	3
S	{}	{}	{s,t,g,w}	{s,t,g,w}
N	{}	{s,t,g,w}	{s,t,g,w}	{s,t,g,w}
V	{}	{e,d}	{e,d}	{e,d}

把FIRST集推广到任意串上

FIRST_S(β1… βn) =

FIRST(N), if β1 == N,

{a}, if β1 == a.

N\FIRST
S	{s,t,g,w}
N	{s,t,g,w}
V	{e,d}

构造LL(1)分析表

N\T	s	t	g	w	e	d
S	0	0	0	0
N	1	2	3	4
V					5	6

LL(1)分析表中的冲突

冲突检测：对N的两条产生式规则N->β和 N-> γ，要求

FIRST_S(β) ∩ FIRST_S(γ) = {}

一般条件下的LL(1)分析表构造

• 首先研究右侧的例子:
  • FIRST_S(X Y Z)
    • 一般情况下需要知道某个非终结符是否可以推出空串
    • NULLABLE
  • 并且一般需要知道某个非终结符后面跟着什么符号
    • 跟随集FOLLOW

NULLABLE集合

定义：

• 非终结符X属于 集合NULLABLE，当且仅当：
  • 基本情况: X->
  • 归纳情况：
    • X-> Y1 … Yn
      • Y1 … Yn是n个非终结符,且都属于NULLABLE集

算法

NULLABLE = {}

while( nullable is still changing )
    foreach(production p: X->β)
        if(β == ε)
            NULLABLE ∪= {X}
        if(β == Y1 .. Yn)
            if(Y1 ∈NULLABLE && ... && Yn ∈ NULLABLE)
                NULLABLE ∪= {X}

上面的算法对应的文法

Z -> d
    | X Y Z
Y -> c
    | 
X -> Y
    | a

NULLABLE	0	1	2
	{}	{Y,X}	{Y,X}

为什么，会出现 Y,X呢？因为 Y 可以推出空串，而 X 可以推出Y，所以X也算到NULLABLE里

FIRST集合的完整计算公式

基于归纳的计算规则：

  * 基本情况:  X-> a
     * FIRST(X)  ∪= {a}
  * 归纳情况：
     * X-> Y1 ... Yn
        * FIRST(X) ∪= FIRST(Y)
        * if Y1 ∈ NULLABLE, FIRST(X) ∪=FIRST(Y2)
        * if Y1, Y2 ∈ NULLABLE, FIRST(X) ∪= FIRST(Y3)

FIRST集的不动点算法

foreach(nonterminal N)
    FIRST(N) = {}

while (some set is changing)
    foreach( production p: N-> β1 ... βn)
        foreach(β1 == a )
            if( β1 == a ... )
                FIRST(N) U= {a}
                break
            if (β1 == M ...)
                FIRST(N) = FIRST(M)
                if(M is not in NULLABLE)
                    break;

Z -> d
    | X Y Z
Y -> c
    | 
X -> Y
    | a

N\FIRST	0	1	2
Z	{}	{d}	{d,c,a}
Y	{}	{c}	{c}
X	{}	{c,a}	{c,a}

这个 下一次循环，我也没有 了解过 “|”后怎么并。

FOLLOW集不动点算法

foreach (nonterminal N)
    FOLLOW(N) = {}

while(some set is changing)
    foreach(production p: N -> β1 ... βn)
        temp = FOLLOW(N)
            foreach(βi from βn downto β1) // 逆序
                if( βi == a)
                    temp = {a}
                if(βi == M ...)
                    FOLLOW(N) ∪= temp
                    if( M is not NULLABLE)
                        temp = FIRST(M)
                    else temp ∪= FIRST

计算例子:

Z -> d
    | X Y Z
Y -> c
    | 
X -> Y
    | a

NULLABLE = {X,Y}

	X	Y	Z
FIRST	{a,c}	{c}	{a,c,d}

N\FOLLOW	0	1	2
Z	{}	{}
Y	{}	{a,c,d}
X	{}	{a,c,d}

看视频说这个 {a,c,d} 是 从第二行， X Y Z 这样推

计算机FIRST_S集合

foreach (nonterminal N)
    FOLLOW(N) = {}

calculte_FIRST_S(production p: N->β1 ... βn)
    foreach( βi from β1 to βn)
        if(βi == a)
            FIRST_S(p) ∪= {a}
            return;
        if(βi == M ...)
            FIRST_S(p) ∪= FIRST(M)
                if(M is not NULLABLE)
                    return;
    FIRST_S(p)  ∪= FOLLOW(N)

Z -> d
    | X Y Z
Y -> c
    | 
X -> Y
    | a

	X	Y	Z
FIRST	{a,c}	{c}	{a,c,d}
FOLLOW	{a,c,d}	{a,c,d}	{}

	0	1	2	3	4	5
FIRST_S	{d}	{a,c,d}	{c}	{a,c,d}	{c,a,d}	{a}

	a	c	d
Z	1	1	0,1
Y	3	2,3	3
X	4,5	4	4

通过LL1分析，主要就是得出一个分析表。

LL(1)分析器

tokens[];
i = 0;
stack = [s]
while(stack != [])
    if(stack[top] is a terminal t)
        if(t == tokens[i++])
            pop();
        else error(.....);
    else if(stack[top] is a nonterminal T)
        pop();
        push(table[T,tokens[i])

LL(1)分析冲突处理

LL(1) 可能会产生冲突，一个对应的位置中可能会有两个数字

E -> E + T
    | T
T -> T * F
    | F
F -> n

示例

	n	+	*
E	0,1
T	2,3
F	4

FIRST_S集合

	0	1	2	3	4
FIRST_S	{n}	{n}	{n}	{n}	{n}

消除左递归

E -> E + T
    | T
T -> T * F
    | F
F -> n

E -> T E'
E' -> + T E'
    |
T -> F T'
T' -> * F T'
    |
F -> n

	n	*	+
E	0
E’		1
T	3
T’		5	4
F	6

提取左公因子

X -> a Y
    | a Z
Y -> b
Z -> c

X -> a X'
X' -> Y
    | Z
Y -> b
Z -> c

LR 分析算法

LL(1)分析算法

从左（L）向右读入程序，最左(L)推导,采用一个(1)前看符号 。

• 优点：
  • 算法运行高效
  • 有现成的工具可用
• 缺点：
  • 能分析的文法类型受限
  • 往往需要文法的改写

自底向上分析算法

• 研究其中最重要也是最广泛的一类
  • LR分析算法（移进-规约算法）
    • 算法运行高效
    • 有现成工具可用
  • 这也是目前最广泛的一类语法分析器的自动生成器中采用的算法
    • YACC,bison, CUP(java), C#yacc, 等

点记号

为了方便标记语法分析器已经读入了多少输入，我们可以引入一个点记号 。

E + 3 ● * 4

文法:

S -> E
E -> E + T
    | T
T -> T * F
    | F
F -> n

生成一个逆序的最右推导

需求两个步骤：

• 移进一个记号到栈顶上，或者
• 归约 栈顶上的n个符号 （某产生式的右部）到左部的非终结符
  • 对产生式 A -> β1 … βn
    • 如果 βn … β1 在栈顶上，则弹出βn .. β1
    • 压入A
• 核心问题，如何确定 移进 和 归约的时机？

算法思想

0: S' -> S$
1: S -> x x T
2: T -> y

分析输入串：x x y $

此 状态 机，LR的状态机也可以直接用二维表，进行表示

	动作(ACTION)			转移(GOTO)
状态\符号	x	y	$	S	T
1	s2			g6
2	s3
3		s4			g5
4	r2	r2	r2
5	r1	r1	r1
6			accept

LR分析表就是上面状态机的一个等价的描述，并不是一个具体的执行过程。

LR(0)分析算法

stack = []
push($)
push(1)
while(true)
    token t = nextToken()

LR(0)分析表构造算法

c0 = closure(S' -> ● S $)  // the init closure
SET = {C0}  // all states
Q = enQueue(C0)  // a queue
while( Q is not empty)
    C = deQueue(Q)
    foreach(x ∈ (N∪T))
        D = goto(C,x)
    if( x ∈N)
        ACTION[C,x] = D
    else GOTO[C,x] = D
    if ( D not ∈ SET)
        SET ∪= {D}
        enQueue(D)

Goto和Closure

goto(C,x)
    temp ={}
    foreach(C's item i: A -> β ● x γ)
        temp ∪= {A -> β x ● γ)
    return closure(temp)

closure(c)
    while(c is still changing)
        foreach(C's item i : A -> β ● B γ)
            C ∪= {B -> ... }

SLR语法分析

LR(0)分析算法

从左(L)向右读入程序,最右(L)推导，不用前看符号来决定产生式的（0个前看符号）

• 优点：

  • 容易实现

• 缺点：

  • 能分析的文法有限
    LR(0)分析算法的缺点

• 对每一个形如 X -> α ● 的项目

  • 直接把 α 归约成 X ,紧跟一个Goto
  • 尽管不会漏掉错误，但会延迟错误发现时机
    • 练习：尝试“x x y x”

• LR(0)分析表中可能包含冲突

问题1：错误定位

问题2：冲突

LR(1)分析算法

越学越迷糊了。现在感觉有点不知所芸。

SLR 分析算法的思想

• 基于LR(0),通过进一步判断一个前看符号，来决定是否执行归约动作。
  • X -> α ● 归约,当且仅当 y ∈ FOLLOW(X)
• 优点：
  • 有可能减少需要归约的情况
  • 有可能需要除去移进-归约冲突
• 缺点：
  • 仍然有冲突出现的可能

SLR分析表中的冲突

LLR(1)项目

• [ X -> α●β,a] 的含义是:
  • α 在栈顶上
  • 剩余的输入能够匹配 βα
• 当归约 X -> αβ时，α是前看符号
  • 把’reduce by X -> αβ’，填入ACTION[s,a]

LR(1)项目的构造

其他和LR(0)相同，仅闭包的计算不同

对项目[X -> α ●Y β , a]

添加 [Y -> α ● γ, b ]到项目集

其中 b ∈ FIRST_S(βα)

下面这个明天再看一遍，确实是没有看懂。

LALR分析算法

• 把类似项目集进行合并
• 需要修改ACTION 表和 GOTO表,以反映合并的效果

对二义性文法的处理

• 二义性文法无法使用LR分析算法分析
• 有几类二义性文法很容易理解，在LR分析器的生成工具中，可以对它们特殊处理
  • 优先级
  • 结合性
  • 悬空else

E -> E + E
    | E * E
    | n

LR(1)分析工具

语法分析器的实现方法

• 手工方式
  • 递归下降分析器
• 使用语法分析器的自动生成器
  • LL(1), LR(1)
• 两种方式在实际的编译器中都有广泛的应用
  • 自动的方式更适合快速对系统进行原型

YACC

Yet Another Compiler-Compliler

用户代码和Yacc声明：可以在接下来的部分使用

语法规则：上下文无关文法及相应主义的应用

用户代码：用户提供代码

%{
  #include <stdio.h>
  #include <stdlib.h>
  int yylex();
  void yyerror();

  %}
%left '+'

%%

lines: line
  | line lines
;

line: exp '\n';

exp: n
  | exp '+' exp
;

n: '1' | '2' | '3' | '4' | '5' |'6'|'7'|'8'|'9'|'0';

%%

int yylex(){
  return getchar();
}

void yyerror(char *s) {
  fprintf(stderr, "%s\n", s);
  return;
}

int main(int argc, char ** argv) {
  yyparse();
  return 0;
}

语法制导翻译

• 编译器在做语法分析的过程中,除了回答程序语法是否合法外,还必须完成后续工作。
  • 包括，但不限于
    • 类型检查
    • 目标代码生成
    • 中间代码生成
    • 。。。
  • 这些后续工作一般可以通过语法制导翻译完成。

LR分析中的语法制导翻译

if(action[s,t] == 'ri' )
    pop(βi)
    state s' = stack[top]
    push(x)
    push(goto[s' , x])

X -> β1 a1
    |β2 a2
    |β3 a3
    ... βi ai
    |βn an

示例

计算表达式的值

E -> E + E { E = E1 + E2}
    | n   {E = n }     

对应后序遍历的序

接下来看Yacc中的实现示例

主要看后面添加的花括号的内容

%{
  #include <stdio.h>
  #include <stdlib.h>
  int yylex();
  void yyerror();

  %}
%left '+'

%%

lines: line
  | line lines
;

line: exp '\n' { printf("value:%d\n",$1); }
;

exp: n               {$$=$1;}
| exp '+' exp    {$$=$1 + $3;}
;

n: '1'  {$$=1;}
| '2'   {$$=2;}
| '3'   {$$=3;}
| '4'   {$$=4;}
| '5' |'6'|'7'|'8'|'9'|'0';

%%

int yylex(){
  return getchar();
}

void yyerror(char *s) {
  fprintf(stderr, "%s\n", s);
  return;
}

int main(int argc, char ** argv) {
  yyparse();
  return 0;
}

语法翻译原理

• 给每条产生式规则附加一条语义动作
  • 一个代码片段
• 语义动作在产生式“归约”时执行
  • 即由的右部的值计算左部的值
  • 以自底向上的技术为例进行讨论
    • 自顶向下的技术与此类似

if(action[s,t] == 'ri' )
    pop(βi)
    state s' = stack[top]
    push(x)
    push(goto[s' , x])

在分析栈中维护三元组： <symbol, value, state>

其中symbol是终结符或非终结符，value是symbol所拥有的值，state是当前的分析状态

X -> β1 a1
    |β2 a2
    |β3 a3
    ... βi ai
    |βn an

示例

图里面 主要展示的是其实际的操作过程，以及在数据结构中的形式。

这种入栈出栈的操作，就是实际代码中的操作过程。

抽象语法树

分析树

• 分析树编码了句子推导的过程
• 但包含了一些不必要的信息
  • 这些结点会占用额外的内存空间

• 对于表达式而言，编译只需要知道运算符和运算数
  • 优先级、结合性 等已经在语法分析部分处理掉了
• 对于语句、函数等语言其他构造而言也一样
  • 例如：编译器不关心赋值符号， = 和:= 是一样的

抽象语法树

大概意思就是分析树这一坨太大了，要使用 抽象语法来扩充一下思考

具体语法和抽象语法

• 具体语法是语法分析器使用的语法
  • 必须适合于语法分析， 如各种分隔符、消除左递归、提取左公因子，等
• 抽象语法是用来表达语法结构的内部表示
  • 现代编译器一般采用抽象语法作为前端（词法语法分析）和后端（代码生成）的接口

抽象语法数据结构

• 在编译器中,为了定义抽象语法树，需要使用实现语言来定义一组数据结构
  • 和实现语言密切相关
• 早期的编译器有的不采用抽象语法数据结构
  • 直接在语法制导翻译中生成代码
  • 现代编译器一般采用抽象语法树作为语法分析器的输出
    • 更好的系统支持
    • 简化编译器的设计

数据结构定义

文法

E -> n
    | E + E
    | E * E

enum kind {E_INT, E_ADD, E_TIMES};

struct Exp {
    enum kind kind;            
}

struct Exp_Int{
    enum kind kind;
    int n;
}

struct Exp_Add {
    enum kind kind;
    struct Exp*left;
    struct Exp *right;
}

struct Exp_Times  {
    enum kind kind;
    struct Exp *left;
    struct Exp *right;
}

“构造函数”的定义

struct Exp_Int * Exp_Int_new(int n) {
    struct Exp_Int *p = malloc(sizeof(*p));
    p->kind = E_INT;
    p->n = n;
    return n;
}

struct Exp_Add *Exp_Add_new(struct Exp *left, struct Exp *right) {
    struct Exp_Add *p = malloc(sizeof(*p));
    p->kind = E_ADD:
    p->left = left;
    p->right = right;
    return p;
}

优美打印

指的是 读出来什么样的公式，那么打印出来也是什么样的公式

抽象语法树的自动生成

LR分析中生成抽象语法树

• 在语法动作中，加入生成语法树的代码片段
  • 片段一般是语法树的“构造函数”
• 在产生式归约的时候，会自底向上构造整棵树
  • 从叶子到根

E -> E + E {$$ = Exp_Add_new($1, $3)}
    | E * E {$$ = Exp_Times_new($1, $3)
    | n     {$$ = Exp_Int_new($1); }

源代码信息的保留和传播

• 抽象语法树是编译器前端和后端的接口
  • 程序一旦被转换成抽象语法树，则源码即被丢弃
  • 后续的阶段只处理抽象语法树
• 所以抽象语法树必须编码足够多的源代码信息
  • 例如，它必须编码每个语法结构在源代码中的位置（文件、行号、列号等）
    • 这样，后续的检查阶段才能精确的报错
    • 或者获取程序的执行刨面
  • 抽象语法树必须仔细设计！

示例：位置信息

struct position_t{
    char *file;
    int line;
    int column;
}

struct Exp_Add {
    enum kind kind;
    Exp *left;
    Exp *right;
    struct position_t from;
    struct position_t to;
}

语义分析

语义分析的任务

语义分析器 -> 中间件表

• 语义分析 也称为类型检查、上下文相关分析
• 负责检查程序（抽象语法树）的上下文相关的属性：
  • 这是具体语言相关的，典型的情况包括：
    • 变量 在使用前先进行声明
    • 每个表达式都有合适的类型
    • 函数调用和函数的定义一致
    • …. (无法穷尽)

主义分析的示例

通过下面的错误代码，来思考 上下文有关文法

void f (int *p)
{
    x += 4;
    p(23);
    "hello" + "world";
}

int main()
{
    f() + 5;
    break;

    return;
}

程序语言的语义

• 传统上，大部分的程序设计语言都采用自然语言来表达程序语言的语义
  • 例如：对于“+”的运算
    • 要求左右操作数都必须是整形数
• 编译器的实现者必须对语言中的语义规定有全面的理解
  • 主要的挑战是如何能够正确高效的实现
  • 下面是讲主要问题和解决方案

语义分析的任务

• 语义分析也称为类型检查、上下文相关分析
• 负责检查程序（语法树）的上下文相关的属性：
  • 这是具体语言相关的，典型的情况包括：
    • 变量在使用前先进行声明
    • 每个表达式都有合适的类型
    • 函数调用和函数的定义一致
    • ….

语义检查

C– 语言

文法

E -> n
    | true
    | false
    | E + E
    | E && E

// 类型合法的程序

3 + 4

false && true

// 类型不合法的程序

3 + true

true + false

// 对于这个语言，语义分析的任务是：对给定的表达式e,写一个函数

type check(e);

// 返回表达式e的类型，若类型不合法则报错

示例2

E -> n
    | true
    | false
    | E + E
    | E && E

enum type{INT, BOOL}

enum type check_exp(Exp_t e)
    switch(e->kind)
        case EXP_INT: return INT;
        case EXP_TRUE: return BOOL;
        case EXP_FALSE: return BOOL;
        case EXP_ADD:
            t1 = check_exp(e->left);
            t2 = check_exp(e->right);
            if(t1 != INT || t2 != INT)
                error("Type mistmatch");
            else return INT;
        case EXP_AND:
            t1 = check_exp(e->left);
            t2 = check_exp(e->right);
            if(t1 != BOOL || t2 != BOOL )
                error("Type mistmatch");
            else return BOOL;

变量 声明的处理

// 类型合法的程序
int x;
x + 4
// 类型合法的程序
bool y;
false && y;
// 类型不合法的程序
x + 3
// 类型不合法的程序
int x;
x + false

类型检查算法

文法

P -> D E
D -> T id; D
    |
T -> int
    | bool
    
E -> n 
    | id 
    | true
    | false
    | E + E
    | E && E

enum type {INT, BOOL};
Table_t table;

enum type check_prog(Dec_t d, Exp_t e)
    table = check_dec(d)
    return check_exp(e)

Table_t check_dec(Dec_t d)
    foreach(T id ∈ d )
        table_enter(table, id, T

enum type check_exp((Exp_t e)
    switch(e -> kind)
        case EXP_ID:
            t = Table_lookup(table,id);
            if(id not exist)
                error("id not found")
            else return t

语句处理

void check_stm(Table_t table, Stm_t s)
    switch(s->kind)
        case STM_ASSIGN:
            t1 = Table_lookup(s->id)
            t2 = check_exp(table, e->exp)
            if(t1 != t2)
                error("type mismatch")
            else return INT;
        case STM_PRINTI:
            t = check_exp(s->exp)
            if(t!=INT)
                error("type mismatch")
            else return;
        case STM_PRINTB:
            // ？？？

符号表

• 用来储存程序中的变量相关信息
  • 类型
  • 作用域
  • 访问控制信息
  • …
• 必须非常高效
  • 程序中变量规模会很大

符号表的接口

table.h 文件

#ifndef TABLE_H
#define TABLE_H

typedef ... Table_new();

// 新建符号表
Table_t Table_new();
// 符号表插入
void Table_enter(Table_t, Key_t, Value_t);
// 符号的查找
Value_t Table_lookup(Table_t, Key_t);

#endif

符号表的典型数据结构

// 符号表是典型的字典结构
    symbolTable: key ->
        value
// 一种简单的数据结构的定义（概念上的）:
typedef char *key;
typedef struct value{ 
    Type_t type;
    Scope_t scope;
    // 其他必要字段
}

符号表的高效实现

• 为了高效可以使用哈希表等数据结构来实现符号表
  • 查找是O(1)时间
• 为了节约空间，也可以使用红黑树等平衡树
  • 查找是O(lg N)时间

作用域

int x;
int f(){
    if(4) {
        int x;
        x = 5;
    }
    else {
        int x;
        x =  7;
    }
    x = 8;
}

符号表处理作用域的方法

• 方法#1：一张表的方法
  • 进入作用域时，插入元素
  • 退出作用域时，删除元素
• 方法#2：采用符号表构成的栈
  • 进入作用域时，插入新的符号表
  • 退出作用域时，删除栈顶符号表

示例

名字空间

struct list{
    int x;
    struct list *list;
} *list;

void walk(struct list *list) {
    list:
        printf("%d\n",list->x);
    if(list = list->list)
        goto list;
}

用符号表处理名字空间

• 每个名字空间用一个表来处理
• 以C语言为例
  • 有不同的名字空间
    • 变量
    • 标签
    • 标号
    • ….
  • 可以每类定义一张符号表

其他问题

• 语义分析中要考虑的其它问题：
  • 类型相容性？
  • 错误诊断?
  • 代码翻译

类型相等

• 类型检查问题往往归结为判断两个类型是否相等 t1 == t2 ?

  • 在实际的语言中，这往往是个需要谨慎处理的复杂问题

• 示例1：名字相等 vs 结构相等

  • 对采用名字相等的语言，可直接比较
  • 对采用结构相等的语言，需要递归比较各个域

  struct A {
      int i;
  } x;
  
  struct B {
      int i ;
  } y;
  
  x = y;
  

• 示例2： 面向对象的继承

  • 需要维护类型间继承关系

错误诊断

• 要给出尽可能准确的错误信息
• 要给出尽可能多的错误信息
  • 从错误中进行恢复
• 要给出尽可能准确的出错位置
  • 程序代码的位置信息要从前端保留并传递过来

代码翻译

• 现代的编译器中的语义分析模块，除了做语义分析外，还要负责生成中间代码或目标代码
  • 代码生成的过程也同样是对树的某种遍历
  • 代码翻译将在课程后续讨论
• 因此，语义分析模块往往是编译器中最庞大也最复杂的模块

代码生成

前端

中间端和后端

最简单的结构

这种结构一看就是没有优化过

代码生成的任务

• 负责把源程序翻译成“目标机器”上的代码
  • 目标机器：
    • 可以是真实的物理机器
    • 可以是虚拟机
• 两个重要任务
  • 给源程序的数据分配计算资源
  • 给源程序的代码选择指令

给数据分配计算资源

• 源程序的数据：
  • 全局变量、局部变量、动态分配等
• 机器计算资源：
  • 寄存器、数据区、代码区、栈区、堆区
• 根据程序的特点和编译器的设计目标，合理的为数据分配计算资源
  • 例如：变量放在内存里还是寄存器里？

寄存器的数量是有限的，所以如何利用是很重要的问题。

给代码选择合适的机器指令

• 源程序的代码：
  • 表达式运算、语句、函数等
• 机器指令：
  • 算术运算、比较、跳转、函数调用返回
• 用机器指令实现高层代码的语义
  • 等价性
  • 对机器指令集体系结构（ISA）的熟悉

路线图

• 为了讲解代码生成的重要问题和解决方案，研究两种不同的ISA上的代码生成技术
  • 栈计算机Stack
  • 寄存器计算机Reg

栈式计算机

• 栈式计算机历史上非常流行

  • 上世纪70年代有很多栈式计算机

• 因为效率问题，今天已经退出历史舞台

• 还讨论栈式计算机民的代码生成技术的原因是：

  • 给栈式计算机生成代码是最容易的
  • 仍然有许多栈式的虚拟机
    • Pascal P Code
    • VJM
    • Postscript
    • ….

栈式计算机的结构

• 内存
  • 存放所有的变量
• 栈
  • 进行运算的空间
• 执行引擎
  • 指令的执行

计算机的指令集

// 指令的语法

S -> push NUM
    | load x
    | store x
    | add
    | sub
    | times
    | div
    

push Num:
    top ++;
    stack[top] = NUM;

load x:
    top ++;
    stack[top] = x;

store x:
    x = stack[top];
    top --;
    
add:
    temp = stack[top-1] + stack[top];
    top -= 2;
    push temp;

面向栈计算机的代码生成

递归下降代码生成算法：从C – 到Stack

指令语法

s -> push NUM
    | load x
    | store x
    | add
    | sub
    | times
    | div

P -> D S 
D -> T id; D
    |

T -> int 
    | bool

S -> id = E
    | printi(E)
    | printb(E)

E -> n
    | id
    | true
    | false
    | E + E
    | E && E

递归下降代码生成算法：表达式的代码生成

// 不变式，表达式的值总是在栈顶

Gen_E(E e )
    switch(e)[
        case n: emit ("push n");break;
        case id: emit("load id");break;
        case true: emit("push 1");break;
        case false: emit("push 0");break;
        case e1 + e2:
            Gen_E(e1);
            Gen_E(e2);
            emit("add");
            break;
        case ....

递归下降代码生成算法：语句的代码生成

Gen_S(S s)
    switch(s)
        case id = e: Gen_E(e);
            emit("store id")
            break;
        case printi(e): Gen_E(e`);
            emit("printi")
            break;
        case printb(e): Gen_E(e`);
            emit("printb")
            break;

递归下降代码生成算法：类型的代码生成

Gen_T(T t)
    switch(t)
        case int: emit(".int");
            break;
        case bool: emit(".int");
            break;

递归下降代码生成算法：变量声明的代码生成

Gen_D(T id; D)
    Gen_T(T);
    emit("id");
    Gen_D(D)

示例

下面是视频中老师的C–，栈式计算机的代码

int x;
int y;
int z;

x= 10;
y = 5;
z  = x + y;
y = z *x;

翻译成下面的代码

.int x
.int y
.int z

1: push 10
3: store x
4: push 5
6: push x
7: push y
8: add
9: store z
10: load z
11: load x
12: times
13: store y

如何运行生成的代码

• 找一台真实的物理机（这玩意就是古董
• 写一个虚拟机（解释器）来运行翻译后的程序
  • 类似于JVM
  • JIT 难道是将翻译后的代码直接编译成x86的机器码，所以才快？这方面有提到，但我没有太理解
• 在非栈式计算机上进行模拟：
  • 例如： 可以在x86上模拟栈式计算机的行为
    • 用x86的调用栈模拟栈

代码生成：寄存器计算机及其代码生成

• 寄存器计算机是目前最流行的机器体系结构之一
  • 效率很高
  • 机器体系结构规整
• 机器基于寄存器架构：
  • 典型的有16、32或更多个寄存器
    • 所有操作都在寄存器中进行
  • 访问都通过load/store进行
    • 内存不能直接运算

寄存器计算机Reg的结构

• 内在
  • 存放溢出的变量
• 寄存器
  • 进行运算的空间
  • 假设有无限多个
• 执行引擎
  • 指令的执行

寄存器计算机的指令集

// 指令的语法

s -> movn n,r
    | mov r1, r2
    | load [x], r
    | store r, [x]
    | add r1, r2, r3
    | sub r1, r2, r3
    | times r1, r2, r3
    | div r1, r2, r3

变量的寄存器分配伪指令

• Reg机器只支持一种数据类型int，并且给变量 x分配寄存器的伪指令是
  • .int x
• 在代码生成阶段，假设Reg机器上有无限多的寄存器
  • 因此每个声明变量和临时变量都会占用一个（虚拟）寄存器
  • 把虚拟寄存器分配到物理寄存器的过程称为寄存器分配

递归下降代码生成算法 从C – 到Reg

递归下降代码生成算法：表达式的代码生成

递归下降代码生成算法：语句的代码生成

类型的代码生成

示例

int x;
int y;
int z;

x = 1+2+3+4;
y = 5;
z = x+y;
y = z*x;

如何运行生成的代码

• 写一个虚拟机（解释器）
• 在真实的物理机上运行
  • 需要进行寄存器分配

小结

总得来说，就是词法分析、词法分析、语义分析后，这个代码是正常的了，也可以保证代码至少是在规则是没有问题的了。那么就可以开始生成代码了。

这里生成代码，使用的是指令形式。其实就是汇编。把他的C–代码生成汇编代码。

因为语言非常简单，所以工作量不大。后面我也理应当采取这种方式，先熟悉搞明白怎么开发一个新语言再下一步。

中间代表

中间代表的地位和作用

• 树和有向无环图（DAG）
  • 高层表示，适用于程序源代码
• 三地址码（3-address code)
  • 低层表示，靠近目标机器
• 控制流图（CFG）
  • 更精细的三地址码，程序的图状表示
  • 适合做程序分析、程序分析等
• 静态单赋值形式（SSA）
  • 更精细的控制流图
  • 同时编码控制流信息和数据流信息
• 连续传递风格（CPS）
  • 更一般的SSA

为什么要划分成不同的中间表

• 编译器工程上的考虑

  • 阶段划分：把整个编译器过程规划成不同的阶段
  • 任务分解：每个阶段只处理翻译过程的一个步骤
  • 代码工程：代码更容易实现、维护、和演进。

• 程序分析和代码优化的需求

  • 两者都和程序的中间表示密切相关
    • 许多优化在特定的中间表示上才可以或才容易进行
  • 后面会讲

通用编译器语言？

因为很难存在这个玩意，所以需要针对每个平台不同的CPU设计一套编译器。

所以可以通过研究中间表，让其生成一套中间表，再把中间表生成对应不同平台的编译器，但好像没有实现。

路线图

• 全面讨论中间表示涉及的重要问题和解决方案
  • 详细介绍现代编译器中几种常用的重要中间表示
    • 三地址码
    • 控制科
    • 静态单赋值形式
  • 详细介绍在中间表示上做程序分析的理论和技术
    • 控制流分析
    • 数据流分析
• 为下一部分讨论代码优化打下基础

三地址码

使用三地址码的编译器结构

三地址码的基本思想

• 给每个计算结果和中间变量命名
  • 没有复合表达式
• 只有最基本的控制流
  • 没有各种控制结构
  • 只有 goto, call等
• 所以三地址码可以看成是抽象的指令集
  • 通用的RISC

示例

定义

三地址码-数据结构

um instr_kind {INSTR_CONST, INSTR_MOVE, ...};

struct Instr_t {enum instr_kind kind;};

struct Instr_Add {
    enum instr_kind kind;
    char *x;
    char *y;
    char *z;
}

struct Instr_Move {
    
};

从C–生成三地址码

语法如下

P -> F*
F -> x ((T id,)*) { (T id;) * S* }
T -> int
    | bool
S -> x = E
    | printi (E)    
    | printb (E)
    | x (E1, ... , En)
    | return E
    | if (E, S*, S*)
    | while(E, S*)
    
E -> n
    | x
    | true
    | false
    | E + E
    | E && E

// 要写如下几个递归函数
Gen_P(P)  Gen_F(F)  Gen_T(T)   Gen_S(S)  Gen_E(E)
    

递归下降生成算法：语句的代码生成（I)

Gen_S(S s)
    switch(s )
        case x =e :
            x1 = Gen_E(e);
            emit("x = x1");
            break;
        case printi(e):
            x = Gen_E(e);
            emit("printi(x)");
            break;
        case printb(e):
            x = Gen_E(e);
            emit("printb(x)");
            break;
        case x(e1, ... en):
            x1 = Gen_E(e1);
            ...;
            xn = Gen_E(en);
            emit("x(x1,...,xn)");
            break;
        case return e:
            x = Gen_E(e);
            emit("return x")
            break;
        case if(e, s1, s2):
            x = Gen_E(e);
            emit("Cjmp(x,L1, L2)");
            emit("Label L1:");
            Gen_SList(s1);
            emit("jmp L3");
            emit("Label L2:";
            Gen_Slist(s2);
            emit("jmp L3");
            emit("Label L3:");
            break;
            

小结

• 三地址码的优点
  • 所有操作都是原子的
    • 变量！没有复合结构
  • 控制流结构被简化了
    • 只有跳转
  • 是抽象的机器代码
    • 向后做代码生成更容易
• 三地址码的不足：
  • 程序的控制流信息是隐匿的
  • 可以做进一步的控制流分析

控制流图

使用控制流图的编译器结构

控制结构

评论

• 程序控制流图表示带来了很多好处：
  • 控制流分析：
    • 分析程序时，内部结构很重要
      • 典型问题“程序中是否存在循环”
  • 可以进一步进行其他分析
    • 数据流分析
      • 典型的问题“程序第5行的变量x可能是什么值”
• 现代编译器早阶段就会做控制流分析
  • 方便后续阶段分析

基本概念

• 基本块：是语句一个序列，从第一条执行到最后一条
  • 不能从中间进入
  • 不能从中间退出
    • 即跳转指令只能出现在最后
• 控制流图是一个有向图 G=(V,E)
  • 节点V: 是基本块
  • 边E：是基本块之间的跳转关系

控制流图的定义

s -> x = n
    |x = y + z
    | x = y
    | x = f (x1, x2, ... , xn)
J -> jmp L
    | cjmp(x,L1,L2)
    | return x
B -> Label L;
    S1; S2; ... Sn;
    J

F ->  x()     {B1, .. Bn}

P -> F1, ... Fn

数据结构的定义

struct Block {
    Label_t label;
    List_t stms;
    Jump_t j;
}

// 其他的要自己写，我哪会这玩意儿啊

如何生成控制流图

• 可以直接从抽象语法树生成：
  • 如果高层语言具有特别规整控制流结构的话较容易
• 也可以先生成三地址码，然后再生成控制流图
  • 对于像C这位的语言更合适
    • 包含像goto这样非结构化的控制流语句
  • 更加通用

由三地址生成控制流图算法

List_t stms; // 三地址码所有语句（线性扫描）
List_t blocks = {}; // 控制流图中的所有基本块
Block_t b=  Block_fresh(); // 一个初始的空的基本块

scan_stms()
    foreach(s ∈ stms)
        if(s is "Label L") // s是标号
            b.label = L;
        else (s is some jump) // s 是跳转
            b.j = s;
            blocks ∪= {b};
            b = Block_fresh(); 
        else 
            b.stms ∪= {s} ; // s是普通指令

控制流图的基本操作

• 标准的图论算法可以使用在控制流图上
  • 遍历算法、生成树、必经节点结构、等
• 图节点的顺序有重要的应用：
  • 拓扑序、逆拓扑序、近似拓扑序、等等（这个我不了解）

死块基本删除优化的示例

int f(){
    int i= 3;
    while(i < 10) {
        i = i +1;
        printi(i);
        continue;
        printi(i);
    }
    return 0;
}

上面是需要优化的代码，里面有死块，可以使用控制流图的优势进行优化

把L3这个没有入口的块给删了

// 输入：控制流图q
// 输出：经过死基本块删除后的控制流图

dead_blocks_elim(g)
    dfs(g)
    for(each node n in g)
        if(! vistited(n))
            delete(n);

数据流分析

经典优化

优化的一般模式

• 程序分析
  • 控制流分析、数据流分析、依赖分析
  • 得到被优化程序的静态保守信息
    • 是对动态运行行为的近似
• 程序重写
  • 以上一步得到的信息制导对程序的重写

静态保守

我的直观感觉就是把一个流程里所有会出现的常量都找出来然后在后面，进行赋值的时候就可以更快

问题：能把 y替换成3吗，如果能，这被称为常量优化

但若 x是 程序输入的话，运行时才能知道值，所以编译器只能采用静态能够获得的信息对程序做保守估计：“L_2可能会执行”

数据流分析

• 通过对程序代码进行静态分析，得到关于程序数据相关的保守信息
  • 必须保证程序分析的结果是安全的
• 根据优化的目标不同，需要进行的数据流分析也不同

两种具体的数据流分析：到达定义分析、活性分析

达到定义

定义(def):对变量的赋值
使用(use):对变量值的读取

达到定义：对每个变量的使用点，有哪些定义可以到达？（即：该变量 是在哪里赋值）

数据流方程 【不会】

大概是两个 代表数据流的相“并、交、加、减”得出一个新的集合（目前的理解是这样的）

对任何一条定义：

[d: x = …]

给出两个集合：

gen[d: x=…] = {d}

x的所有定点

kill[d: x= …] = defs[x] - {d}

like this: defs[y] = {1,4,5}

数据流方程：
（后面有时间再折腾一下怎么写公式，这个学了又忘，主要是不常用）

从数据流议程到算法

// 算法：对一个基本块的到达定义算法
// 输入：基本块中所有的语句
// 输出：对每个语句计算in和out两个集合

List_t stms; // 一个基本块中所有的语句
set = {}; // 临时变量，记录当前语句中s的in集合
reaching_definition()
    foreach(s ∈ stms)
        in[s] = set;
        out[s] = gen[s] ∪ (in[s] - kill[s])
        set = out[s]
        

示例

对一般的控制流图

从数据流方程到不动点算法

// 算法：对所有基本块的达到定义算法
// 输入：基本块中所有的语句
// 输出：对每个语句计算in和out两个集合
List_t stms; // 所有基本块中的所有语句
set = {}
reaching_definition()
    while(some set in[] or out[] is still changing)
        foreach( s ∈ stms)
            foreach(predecessor p of s)
                set ∪= out[p]
            in[s] = set;
            out[s] = gen[s] ∪ (in[s] - kill[s])
            

示例

活性分析

进行活性分析的动机

• 之前讲代码生成的时候，假设机器有无限多个寄存器
  • 简化了代码生成器的算法
  • 对物理机器是一个坏消息
    • 机器只能是有限多个寄存器
      • 必须把无限多个寄存器分配到有限多个寄存器
• 这是 寄存器分配优化 的任务
  • 需要进行活性分析

示例

意思是 多个变量 ，要使用同一个寄存器，所以他们的使用的时间是不能重合的。如果重合了，就需要两个寄存器。

a = 1
b = a + 2
c = b + 3
return c

活跃信息给出了活跃区间的概念。

活跃区间互不相交，所以三个变量可交替使用同一个寄存器。

示例

a = 1
↓ {a}
b = a + 2
↓ {b}
c = b + 3
↓ {c}
return c

寄存器分配
a => r
b => r
c => r
代码重写：

r =1 
r = r + 2
r = r + 3
return r

数据流方程

对任何一条语句： [d: s]

给出两个集合:

gen[d: s] = {x | 变量x在语句s中被使用}
kill[d: s] = {x| 变量x在语句s中被使用}

1: x = y + z
2: z = z + x

基本块后向的数据流方程:

这个的目的就是求 其生存时间，但不过用的是数学方程来求的。
从底向上求， 按照 上面的公式 in[S] = gen[S] ∪ (out[S] - kill[S]) 来求。

一般的数据流方程

• 方程：
  
• 同样给出不动点算法
  • 从初始 的空集{} 出发
  • 循环到没有集合变化为止

示例

下面这张图要根据上面的公式，然后一步步的计算代码中的in/out，然后就可以得到左边的表里面的数据。

干扰图

干扰图是一个无向图G=(V,E):

1. 对每个变量构造无向图G中一个节点；
2. 若变量x，y同时活跃，在x、y间连一条无向边。

可以根据下面的图推出上面的干扰图。

代码优化

基本概念

优化的位置

什么是代码优化？

• 代码优化是对被优化的程序进行一种主义保持的变换
• 语义保持：
  • 程序的可观察行为不能改变
• 变换的目前是让程序能够比变换前：
  • 更小
  • 更快
  • cache行为更好
  • 更节能
  • 等等

不存在“完全优化”

• 等价于停机问题：
  • 给定程序p，把Opt(p) 和 下面的程序比较：

    L:
        jmp L
    

这被称为，“编译器从业者永不失业定理”

代码优化很困难

• 不能保证优化总能产生“好”的结果
• 优化的顺序和组合很关键
• 很多优化问题是非确定的
• 优化正确性论证很微妙

正确的观点

• 把该做对的做对
  • 不是任何程序都可以同概率的出现
    • 能处理大部分情况的优化，就可以接受
• 不期待完美编译器
  • 如果一个编译器有足够多的优化，则就是一个好的编译器

路线图

• 前端优化
  • 局部的、流不敏感的
  • 常量折叠、代数优化、死代码删除等
• 中期优化
  • 全局的、流敏感的
  • 常量传播、扶风传播、死代码删除、公共字表达式删除等
• 后端优化
  • 在后端进行
  • 寄存器分配、指令调度、窥孔优化等

前端优化

前端优化的位置

常量折叠

• 基本思想：
  • 在编译期计算表达式的值
    • 例如： a = 3 + 4 == > a =8
    • 例如： if(true && false) == > if(false)
• 可以在整形、布尔型、浮点型等数据类型上进行

算法

// 语法制导的常量折叠算法
const_fold(Exp_t e)
    while(e is still shrinking)
        switch(e->kind)
            case EXP_ADD:
                Exp_t l = e->left;
                Exp_t r = e->right;
                if( l->kind = EXP_NUM && r -> kind = EXP_NUM)
                    e = Exp_Num_new(l->value + r->value);
                break;
            default;
                break;

小结

(这里应该是漏了一节视频)

• 容易实现、可以在语法树或者中间表示上进行
• 通常被实现成公共子函数被其它优化调用
• 必须要很小心遵循语言的语义
  • 例如：考虑溢出或异常
    • 例子： oxffff ffff + 1 == > 0 (??? ) （我也不知道

代数化简

• 基本思想：
  • 利用代数系统的性质对程序进行化简
  • 示例：
    • a = 0 + b -> a =b
    • a = 1*b -> a = b
    • 2 * a = a + a (强度消弱)
    • 2 * a = a << 1 (强度消弱)
• 同样必须非常仔细的处理语义
  • 示例：(i-j) + (i-j) ==> i + i - j -j

算法

(后面有必要再补一下，把高等数学用程序来表示，然后学好高等数学、线代、离散，仅为更好的写出来程序)

// 代数化简的算法
alg_simp(Exp_t e)
    while(e is still shrinking)
        switch(e -> kind)
            case EXP_ADD:
                Exp_t l = e->left;
                Exp_t r = e->right;
                if(l->kind = EXP_NUM && l -> value == 0) 
                    e =r;
                break;
            case ...: ...;

死代码(不可达代码)删除

• 基本思想
  • 静态移除程序中不可执行的代码
  • 示例：
    if (false)
    s1;
    else s2; => s2;
    (就是通过语义分析，删掉那些不会执行的代码)
• 在控制流图上也可以进行这些优化（在那个有向图中直接可以看出来） ，因为控制流也是有向图。但在早期做这些优化可简化中后端

算法

deadcode(Stm_t s)
    while(s is still shrinking)
        switch (s->kind)
            case STM_IF:
                Exp_t e = s->condition;
                if(e->kind = EXP_FALSE)
                    s = s->elsee;
                break;
            case ...:...;

中间表示上的优化

• 依赖于具体所使用的中间表示
  • 控制流图（CFG）、控制依赖图（CDG）、静态单赋值形式（SSA）、后续传递风格（CPS）等。
• 共同的特点是需要进行程序分析
  • 优化是全局进行的，而不是局部
  • 通用的模式是：程序分析 → 程序重写
• 在这部分中，我们将基于控制流图进行讨论
  • 但类似的技术可以用于其它类型的中间表示

优化的一般模式

• 程序分析
  • 控制流分析，数据流分析，依赖分析。。。。
  • 得到被优化程序的静态保守信息
    • 是对动态运行行为的近似
• 程序重写
  • 以上一步得到的信息制导对程序的重写

常量传播

先进行达到定义分析，如果这个定义 “x=3” 是唯一能够达到 “a=3”的定义，那么可以用这个进行替换。

常量传播算法

// 常量传播算法
const_prop(Prog_t p)
    // 第一步：程序分析
    reaching_definition(p);
    // 第二步：程序改写
    foreach(stm's in p:y = x1, ... ,xn)
        foreach(use of xi in s)
            if(the reaching def of xi is unique: xi =n)
                y = x1, .... , xi -1, n , xi+1, ... ,xn

讨论

拷贝传播

死代码删除

这个我没有看出来跟之前的死代码优化有什么变化。
意思就是通过活必分析，判断这一块代码执行后有对结果有没有什么影响。
在不影响语义的情况下，可以删掉。（这样理解是否正确呢？）

算法

// 死代码删除算法
dead_code(Prog_t p)
    // 第一步：程序分析
    liveness_analysis(p);
    // 第二步：程序改写
    foreach(stm s in p: y = ....)
        if (y is NOT in live_out[s])
            remove(s)

完结撒花

这一遍仅是过一下知识点，其实很多点没有听懂。但主要是要过一下知识点。怎么可能通过这一点点视频，就精通一个技术。后面的提升取决于我的做多少个练习。

刻意练习 ，把一个编译器，以不同的方式，不同的语法，进行锻炼。

加油。